Berkson's Paradox

Written for STAT 131.

One of the joys/horrors of TA-ing is that you always encounter things that stumps you as well as your students (especially in probability). Here is a very basic looking problem that stumped me from Introduction to Probability by Joe Blitzstein and Jessica Hwang (Ch2 Q37):

Two different dieseases cause a certain weird symptom: anyone who has either or both of these dieseases will experience the symptom. Let \(D_1 \) be the event of having the first disease, \(D_2 \) be the event of having the second, and \(W \) be the event of having the weird symptom. Suppose \(D_1 \) and \(D_2 \) are independent with \(P(D_j) = p_j \) and that a person with neither disease will have the weird symptom with probability \(w_0 \). Let \(q_j =1-p_j \).

NOTE: Feel free to jump to (d) since this is long.

(a) Find \(P(W)\)

We can use the Law of Total Probability (LOTP).

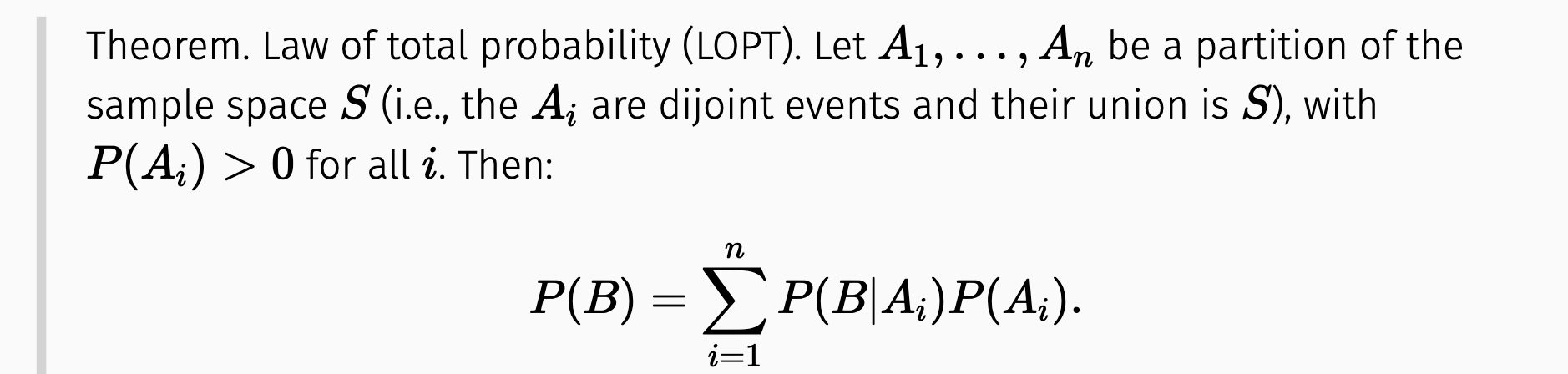
So let \(D_1 \cup D_2 \) be the event that you have at least one disease.
Let \(D_1^c \cap D_2^c \) be the probability that you have neither.

Then

\[ P(W) = P(W \mid D_1 \cup D_2) P(D_1 \cup D_2) + P(W \mid D_1^c \cap D_2^c) P(D_1^c \cap D_2^c) \]

So using the laws of probability you’ve learned: \(P(D_1 \cup D_2) = p_1 + p_2 - p_1p_2 \) And \(P(D_1^c \cap D_2^c)=(1-p_1 )(1-p_2) = q_1q_2\).

Anyone who has at least one of the diseases will have weird symptoms with probability=1. Thus \(P(W \mid D_1 \cup D_2) =1\).
We are given that probability that you have a weird disease without having the disease is \(w_0\). Thus we have \(P(W) = 1 ( p_1 + p_2 - p_1p_2) + w_0 q_1 q_2\).

(b)

Find \(P(D_i \mid W)\)

We need to find the prob. that you have disease \(i \) given weird symptoms Note that using the formula for conditional probability: \[ P(Di \mid W) = \frac{P(D_i \cap W)} {P(W)} = \frac{P( W \mid Di) P(Di)} {P(W)} \]

We already know \(P( W \mid Di)= 1\).

Using result from (a), for \(i=1,2 \) we have:

\[ P(Di \mid W) = \frac{P(D_i)} {P(W)} = \frac{p_i} {( p_1 + p_2 - p_1p_2) +w_0 q_1q_2} . \]

Find \(P(D_1 \cap D_2 \mid W)\)

We need to find the prob. that you have both diseases given weird symptoms We can solve things in a similar fashion: \[ P(D_1 \cap D_2 \mid W) =\frac{P( W \mid D_1 \cap D_2) P(D_1 \cap D_2)} {P(W)} = \frac {P(D_1 D_2)} {P(W)} = \frac{ p_1 p_2 }{( p_1 + p_2 - p_1p_2) +w_0 q_1q_2}.\]

(c) Are \(D_1, D_2 \) conditionally independent on \(W \)?

Note that for conditional independence to be possible we must have \(P(D_1 \cap D_2\mid W) = P(D_1\mid W) P(D_2\mid W). \)
But we have

\[P(D_1\mid W) P(D_2\mid W) = \frac{p_1}{P(W)} \frac{p_2}{P(W)}. \]

This is not generally equal to

\[ P(D_1 \cap D_2 \mid W) = \frac{p_1 p_2}{P(W)}. \]

unless \(w_0=1 \)(see part (d)).

Thus by contradiction, these events are not conditionally independent.

(d) What if \(w_0=0\)?

If \(w_0=0\), we have \[ P(D_1 \cap D_2 \mid W) = \frac{p_1 p_2}{p_1 + p_2 - p_1p_2}.\]

Which is still NOT equal to \[P(D_1\mid W) P(D_2\mid W) = \frac{p_1} {p_1 + p_2 - p_1p_2} \times \frac{p_2} {p_1 + p_2 - p_1p_2}.\] Thus they are not conditionally independent.

Explanation: Two independent events may NOT be conditionally independent

This is a gnarly example of the counter-intuitive nature of probability. This is related to the Berkson’s Paradox!

Note that one way to look at independence of two events \( A, B\) is to think about things this way:

… knowing the outcome of event B has no impact on the likelihood of A happening.

So if two events are dependent then…

… knowing the outcome of event B changes the likelihood of A happening.

In this case, we are given that someone has weird symptoms: \(W \). Then two events we are considering are: \(D_1 \mid W \)and \(D_2 \mid W\). Since we are given \(W \), they must have \(D_1 \)and \(D_2 \)since \(w_0=0\).

Suppose you know that they don’t have \(D_1\). Then they MUST have \(D_2 \) since they have weird symptoms. Hence knowing \(D_1 \mid W \) impacts the likelihood of \(D_2 \mid W\).

The only way \(D_1 \mid W \) and \(D_2 \mid W \) are independent is if \(w_0=1\). In that case \(w_0 q_1q_2 = 1-p_1 -p_2 +p_1 p_2 \) and \(P(W) = (p_1 + p_2 - p_1p_2) + (1-p_1 -p_2 +p_1 p_2) =1 \). Then knowing \(W \)won’t change anything since everyone has weird symptoms.